Notasi Asymptot
Daftar Isi
- Notasi Asimptotik: Urutan Pertumbuhan
- Urutan Pertumbuhan
- Notasi Ω (Omega), Θ (Theta), dan O (Big O)
- Nama-Nama dari Fungsi Pembatas
- Notasi O (Big O)
- Notasi Θ (Big Theta)
- Contoh-Contoh
- Sifat-Sifat
- Apa Yang Diimplikasikan oleh Properti Asimptotik bagi Sebuah Algoritma?
- Kelas Efisiensi Asimptotik Dasar
- Efisiensi Waktu Algoritma Non-Rekursif
- Contoh 1: Elemen Maksimum
- Contoh 2: Masalah Unik Elemen
- Contoh 3: Perkalian Matriks
- Contoh 4: Menghitung Digit Biner
- Download Materi Power Point
- Referensi
Notasi Asimptotik: Urutan Pertumbuhan
Latar Belakang
Misalkan, dalam kasus terburuk, suatu masalah dapat diselesaikan dengan menggunakan dua algoritma yang berbeda, dengan kompleksitas waktu:

Yang mana yang lebih baik?

Solusi: Abaikan konstanta dan suku dengan orde yang rendah
Kita menggunakan Notasi Asimptotik (Ω, Θ, dan O)
Urutan Pertumbuhan
Nilai (beberapa yang bersifat perkiraan) dari beberapa fungsi penting untuk analisis algoritma.
Notasi Ω (Omega), Θ (Theta), dan O (Big O)
%2C-%CE%98-(Theta)%2C-dan-O-(Big-O)-1.jpg)
Nama-Nama dari Fungsi Pembatas

- f(n) = O(g(n)) berarti C x g(n) adalah batas atas dari f(n);
- f(n) = Ω(g(n)) berarti C x g(n) adalah batas bawah dari f(n);
- f(n) = Θ(g(n)) berarti C1 x g(n) adalah batas atas dari f(n) dan C2 x g(n) adalah batas bawah dari f(n).
Notasi O (Big O)
-1.jpg)
f(n) = Ω(g(n)): g(n) adalah batas bawah secara asimptotik untuk f(n). Artinya, f tidak tumbuh lebih cepat daripada g.
Notasi Θ (Big Theta)
.jpg)
f(n) = Θ(g(n)): g(n) adalah batas yang ketat secara asimptotik untuk f(n). Artinya, g(n) adalah batas yang pas untuk f(n).
Contoh-contoh dari Θ (Big Theta)
.jpg)
False, karena C1 dan C2 harus lebih besar dari 0.
Contoh-Contoh
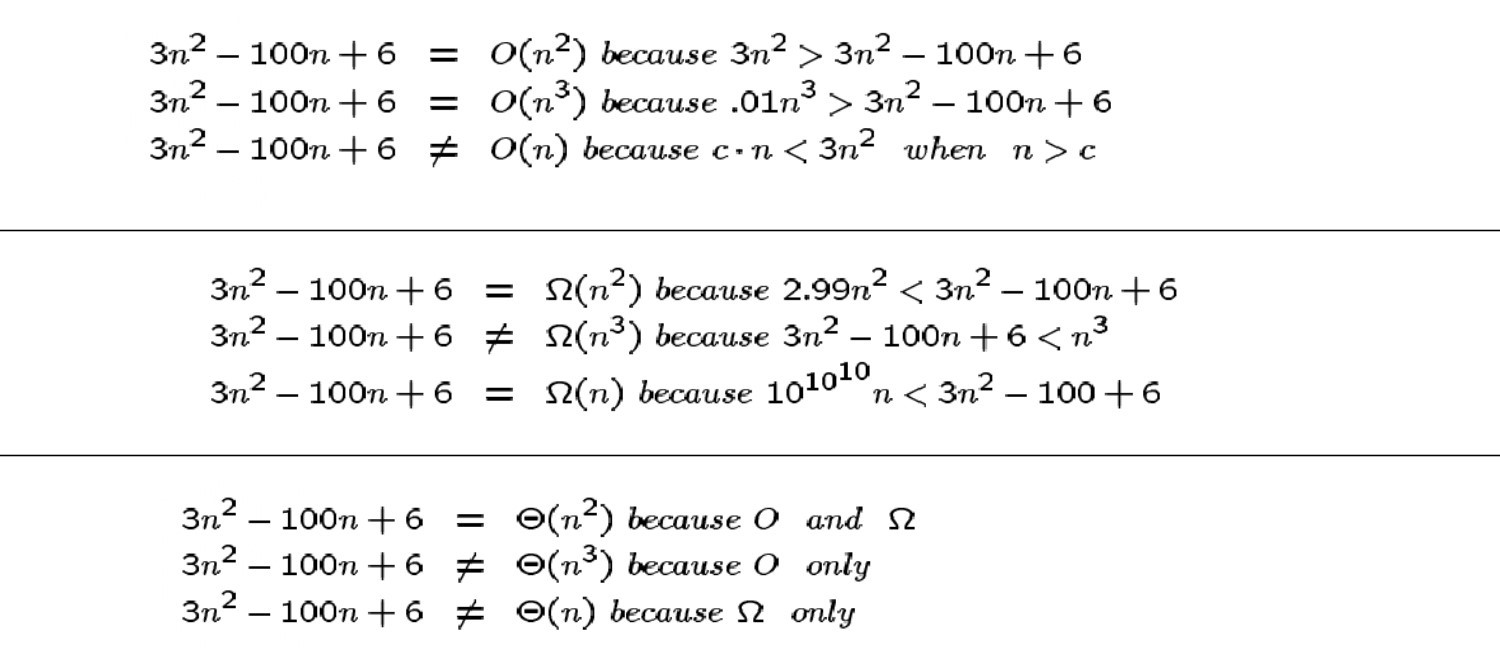
Pikirkan kesetaraan sebagai arti dalam himpunan fungsi.
Sifat-Sifat
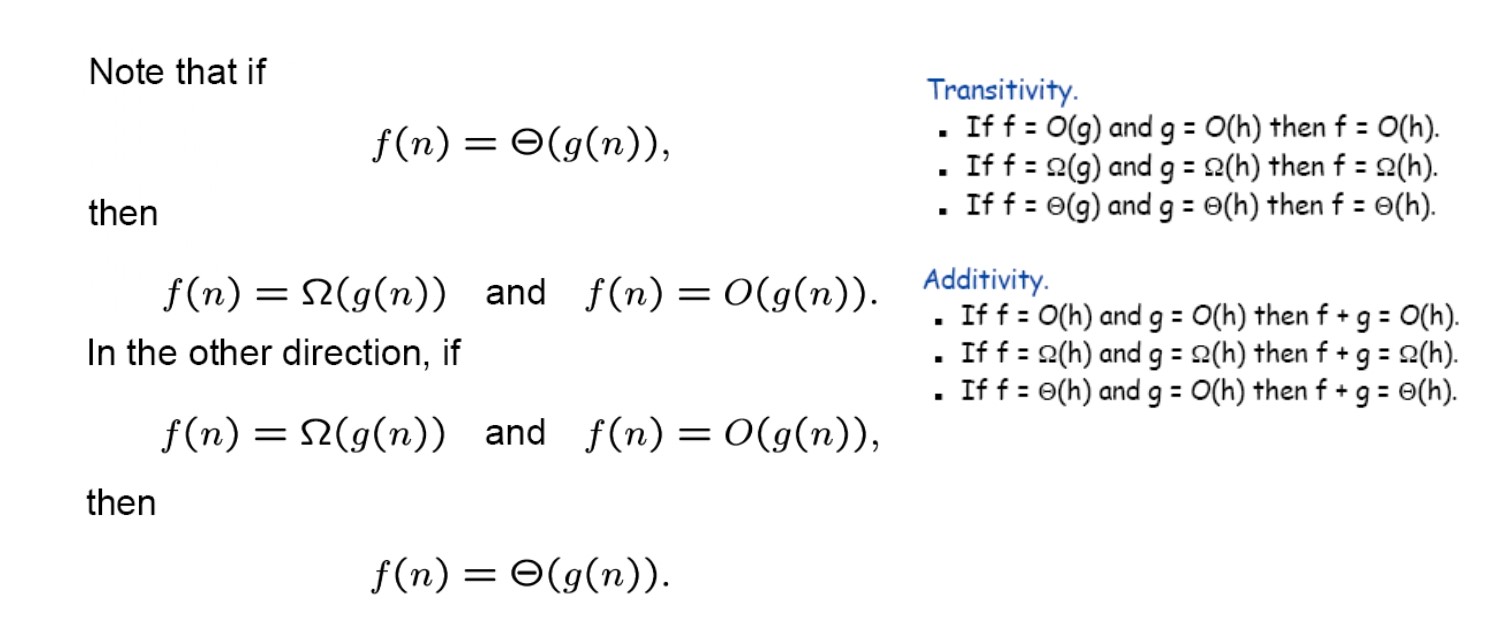
Transitivitas:
- Jika f = O(h) dan g = O(h), maka f = O(h).
- Jika f = Ω(g) dan g = Ω(h), maka f = Ω(h).
- Jika f = Θ(g) dan g = Θ(h), maka f = Θ(h).
Aditivitas:
- Jika f = O(h) dan g = O(h), maka f + g = O(h).
- Jika f = Ω(h) dan g = Ω(h), maka f + g = Ω(h).
- Jika f = Θ(h) dan g = O(h), maka f + g = Θ(h).
Tugas: Berdasarkan definisi Ω, Θ, dan O, buktikan bahwa:
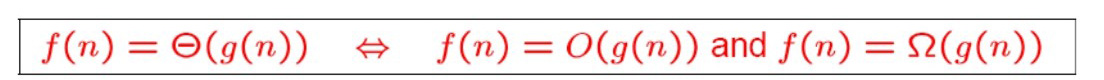
Apa Yang Diimplikasikan oleh Properti Asimptotik bagi Sebuah Algoritma?

Bagaimana efisiensi keseluruhan dari algoritma ini?
Kelas Efisiensi Asimptotik Dasar

Efisiensi Waktu Algoritma Non-Rekursif
Rencana Umum untuk Analisis
- Tentukan parameter n yang mengindikasikan ukuran input
- Identifikasi operasi dasar algoritma
- Tentukan kasus terburuk, rata-rata, dan terbaik untuk input ukuran n
- Atur jumlah kali operasi dasar dijalankan
- Sederhanakan jumlah tersebut menggunakan rumus dan aturan standar
Contoh 1: Elemen Maksimum
Menentukan nilai elemen terbesar dalam sebuah array yang diberikan
Input: Sebuah array A[0..n -1] dari angka real
Output: Nilai elemen terbesar dalam A

Contoh 2: Masalah Unik Elemen
Menentukan apakah semua elemen dalam sebuah array yang diberikan adalah unik atau tidak.
Input: Sebuah array A[0..n -1]
Output: Mengembalikan "true" jika semua elemen dalam A unik, dan "false" jika sebaliknya.

Contoh 3: Perkalian Matriks
Mengalikan dua matriks berukuran n-by-n menggunakan algoritma berdasarkan definisi.
Input: Dua matriks berukuran n-by-n, A dan B
Output: Matriks C = AB

Contoh 4: Menghitung Digit Biner
Input: Sebuah bilangan bulat desimal positif n
Output: Jumlah digit biner dalam representasi biner n, count <- 1

Hal ini tidak dapat diselidiki dengan cara yang sama seperti contoh-contoh sebelumnya.
Download Materi Power Point
https://drive.google.com/drive/folders/16HL651AUf3BihpbvMNgEfEXPwUHbcPz-?usp=drive_link
Referensi
-


