Kompleksitas Algoritma
Daftar Isi
- Pendahuluan
- Running Time (Waktu Eksekusi)
- Contoh Operasi Dasar/Primitif
- Time Complexity (Komplesitas Waktu)
- Tujuan Menghitung Komplesitas Waktu
- Contoh Menghitung Komplesitas Waktu
- Kasus Terbaik (Best Case), Kasus Terburuk (Worst Case), Kasus Rata-rata (Average Case)
- Download Materi Power Point
- Referensi
Pendahuluan
Masalah: diberikan sebuah urutan n elemen yang sudah diurutkan dalam urutan menaik.
Rancanglah algoritma untuk memeriksa apakah nilai x muncul dalam urutan tersebut.
Ide sederhananya: Periksa satu per satu dengan membandingkan x dengan setiap elemen dalam urutan tersebut dari awal hingga akhir.
Running Time (Waktu Eksekusi)
Running Time (waktu eksekusi) dapat didefinisikan sebagai:
- Jumlah operasi dasar/primitif atau 'langkah' yang dieksekusi;
- Waktu tetap untuk setiap baris pseudocode.
Operasi dasar/primitif meliputi:
- Operasi aritmatika - seperti '+', '-', '*', '/' dll.
- Perbandingan logis - seperti '>', '<', '=', '≠', '≤', '≥'
- Panggilan fungsi

Asumsi:
- Operasi dieksekusi secara berurutan.
- Semua operasi memiliki biaya 1 unit.
Waktu eksekusi tergantung pada masukan. Contoh: sebuah urutan yang sudah diurutkan lebih mudah untuk diurutkan.
Waktu eksekusi dari suatu algoritma ditentukan oleh ukuran masukan n.

Contoh Operasi Dasar/Primitif
Berikut adalah contoh basic operation (operasi dasar) atau bisa juga disebut primitive operation (operasi primitif)
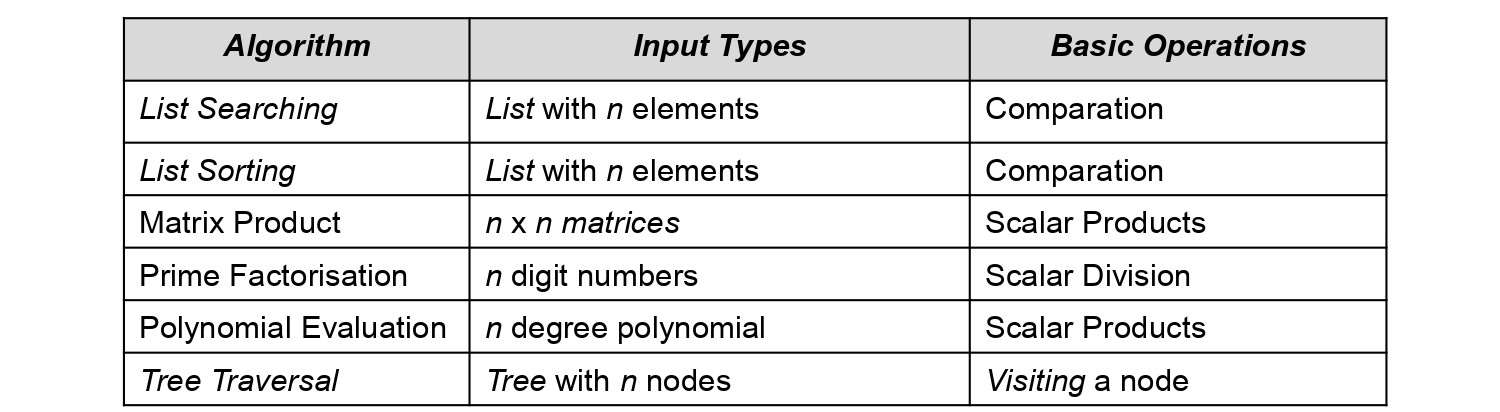
Operasi dasar: operasi yang paling berkontribusi terhadap waktu eksekusi algoritma.
Efisiensi waktu dianalisis dengan menentukan jumlah pengulangan operasi dasar sebagai fungsi dari ukuran input.
Catatan:
- Menghilangkan ketergantungan pada kecepatan komputer kita, yang sebaliknya tidak mungkin untuk diverifikasi dan dibandingkan.
Time Complexity (Komplesitas Waktu)
Kompleksitas suatu algoritma ditentukan oleh jumlah operasi dasar dan berapa kali algoritma menghitung operasi dasar tersebut.
Catatan: Analisis kompleksitas adalah independen terhadap mesin.
Kompleksitas waktu suatu algoritma akan menentukan waktu eksekusi yang bergantung pada ukuran inputnya, yaitu kompleksitas waktu adalah fungsi dari ukuran masukan.

Tujuan Menghitung Komplesitas Waktu
- Untuk memperkirakan berapa lama program akan berjalan
- Untuk memperkirakan input terbesar yang dapat diberikan kepada program dengan wajar
- Untuk membandingkan efisiensi berbagai algoritma
- Untuk membantu fokus pada bagian kode yang dieksekusi sebanyak mungkin
- Untuk memilih algoritma untuk suatu aplikasi
Contoh Menghitung Komplesitas Waktu

Kasus Terbaik (Best Case), Kasus Terburuk (Worst Case), Kasus Rata-rata (Average Case)
Terkadang, dengan memberikan dua input yang berbeda namun memiliki ukuran yang sama, sebuah algoritma dapat memiliki waktu eksekusi yang berbeda.
Contoh:
Misalkan suatu algoritma pengurutan memiliki beberapa input dengan ukuran yang sama tetapi urutan yang berbeda:

Apakah input-input tersebut memberikan waktu eksekusi yang sama?
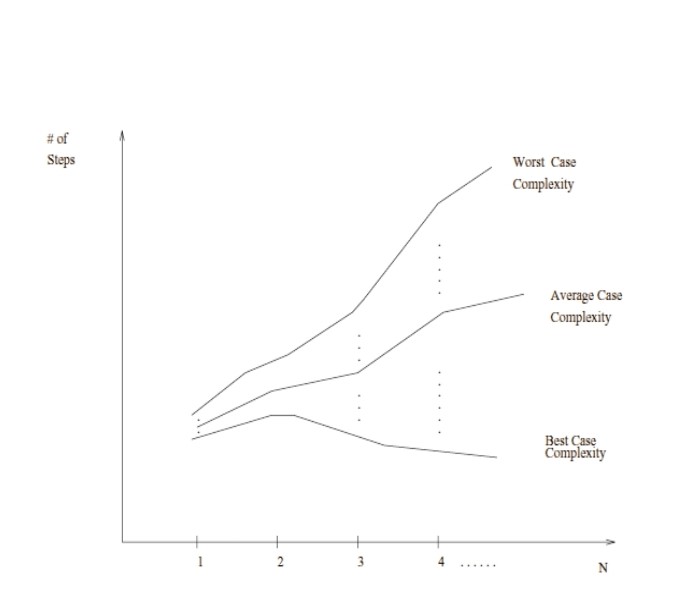
Kasus terburuk kompleksitas algoritma adalah fungsi yang didefinisikan oleh jumlah langkah maksimum yang diambil pada setiap instansi dengan ukuran n.
Kompleksitas kasus terbaik algoritma adalah fungsi yang didefinisikan oleh jumlah langkah minimum yang diambil pada setiap instansi dengan ukuran n.
Kompleksitas kasus rata-rata algoritma adalah fungsi yang didefinisikan oleh jumlah langkah rata-rata yang diambil pada setiap instansi dengan ukuran n.
Catatan: semua kasus tersebut berkaitan dengan algoritma yang sedang dipertimbangkan.
Biarkan In menyatakan himpunan semua input dengan ukuran n dari suatu algoritma dan ????(i) menyatakan jumlah operasi primitif dari algoritma yang sesuai ketika diberikan input i.
Secara matematis, kita dapat mendefinisikan:

di mana p(i) adalah probabilitas i muncul sebagai input dari suatu algoritma.
Download Materi Power Point
https://drive.google.com/drive/folders/1wqVcA-M2pDP8y2pjEmvWEnns1vflvF0V?usp=drive_link
Referensi
-


